Prova: Exame de Matemática Enem 2017
Para decorar uma mesa de festa infantil, um chefe de cozinha usará um melão esférico com diâmetro medindo 10 cm, o qual servirá de suporte para espetar diversos doces. Ele irá retirar uma calota esférica do melão, conforme ilustra a figura, e, para garantir a estabilidade deste suporte, dificultando que o melão role sobre a mesa, o chefe fará o corte de modo que o raio r da seção circular de corte seja de pelo menos 3 cm. Por outro lado, o chefe desejará dispor da maior área possível da região em que serão afixados os doces.
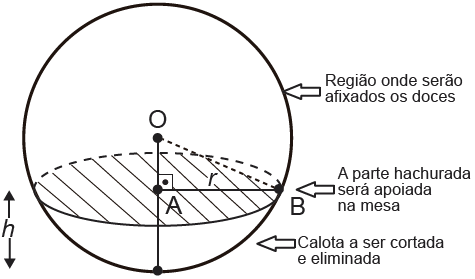
Para atingir todos os seus objetivos, o chefe deverá cortar a calota do melão numa altura h, em centímetro, igual a
- 5 - √91/2
- 10 - √91
- 1
- 4
- 5


Comments