Prova: Exame de Matemática Enem 2017

Um brinquedo infantil caminhão-cegonha é formado por uma carreta e dez carrinhos nela transportados, conforme a figura.

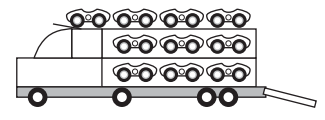
No setor de produção da empresa que fabrica esse brinquedo, é feita a pintura de todos os carrinhos para que o aspecto do brinquedo fique mais atraente. São utilizadas as cores amarelo, branco, laranja e verde, e cada carrinho é pintado apenas com uma cor. O caminhão-cegonha tem uma cor fixa. A empresa determinou que em todo caminhão-cegonha deve haver pelo menos um carrinho de cada uma das quatro cores disponíveis. Mudança de posição dos carrinhos no caminhão-cegonha não gera um novo modelo do brinquedo.

Com base nessas informações, quantos são os modelos distintos do brinquedo caminhão-cegonha que essa empresa poderá produzir?

(A) C_6,4
(B) C_9,3
(C) C_10,4
(D) 6⁴
(E) 4⁶

Teoria Rápida: Análise Combinatória

Combinação Simples (sem repetição)
Dentre n elementos distintos devemos escolher k elementos distintos (k ≤ n), tal que a ordem de escolha não altera o resultado. A fórmula é:

C_n,k = n! / k!(n-k)!

Existem combinações que possuem valores iguais e são chamadas de combinações complementares:

C_n,k = C_n,n-k

Combinação Composta (com repetição)
Neste caso, pode haver repetição de elementos na combinação (não há mais a restrição que k ≤ n). A fórmula é:

CR_n,k = C_n+k-1,n-1

Substituindo os termos:

CR_n,k = (n+k−1)! / k!(n−1)!

Resolução Rápida e Fácil

Cada caminhão terá no mínimo 1 carrinho de cada cor, ou seja, os 6 carrinhos restantes poderão ter qualquer uma das 4 cores disponíveis. Isso corresponde a uma combinação simples com repetição cuja fórmula é:

CR_n,k = C_n+k-1,n-1

Aplicando os valores do enunciado (n=4 e k=6):

CR_4,6 = C_9,3

Gabarito: (B)