Logical reasoning is the ability to draw valid conclusions from a set of assumptions. In everyday discourse, these valid conclusions are often indicated by key words such as: so, then, thus, hence, therefore, consequently, etc.
There is no universal consensus on the exact scope of the subject, but it typically involves the study of arguments, inferences, paradoxes, and fallacies. Historically, it is a field of study of philosophy (since ancient Greece) and mathematics (19th century).
The most common types of logical reasoning are:
- deductive
- inductive
- abductive
Deductive Reasoning
Deductive reasoning means using a set of assumptions to logically deduce valid conclusions. Example:
Main premise: All human beings are mortal.
Minor premise: Socrates is human.
Conclusion: Socrates is mortal.
Combining the general rule "all human beings are mortal" (main premise) with the specific situation "Socrates is human" (minor premise), one can conclude that "Socrates is mortal". This particular type of reasoning - two premises leading to a conclusion - is called syllogism and is a frequent subject in logical reasoning.
Note that deductive reasoning does not provide new information, only rearranges information that is already known in new valid statements. So deductive reasoning is, "If this is true, then this is also true."
Inductive Reasoning
Inductive reasoning aims to find patterns or trends and then generalize and extrapolate. Therefore, it is not certain that a conclusion based on inductive reasoning is 100% valid. A famous hypothesis is:
All swans are white.
This conclusion was obtained after observing that, of a large number of swans, none were black. Consequently, it was assumed that black swans do not exist. Inductive reasoning is therefore a risky form of logical reasoning, since the conclusion can easily be refuted by simply finding a single black swan in this case.
Another typical example of inductive reasoning is number sequences:
6, 9, 12, 15,?
The logical answer to this sequence seems to be 18, but you cannot be 100% sure. There is a possibility that this sequence may represent something strange, different than expected, causing the next sequence number to escape the obvious pattern.
In addition to numerical sequences, it is also possible to have sequences of figures (abstract reasoning). However, the methodology remains the same: find the pattern and extrapolate to find the next figure.
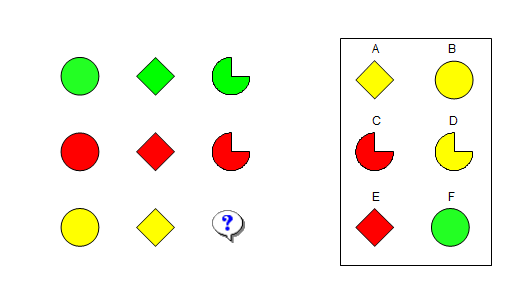
Inductive reasoning is basically this: look at the information given, make a generalization and extrapole. In such cases there will always be the judgment of a generalization, which may or may not be true. While in deductive reasoning, there is no judgment. The conclusions are valid based on the information provided.
Abductive Reasoning
Abductive reasoning is somewhat similar to inductive reasoning. It was initially called "divination" as the conclusions presented are based on probabilities. In abductive reasoning it is assumed that the most plausible conclusion is also the correct one.
Example:
Main premise: The pot is full of yellow balls.
Minor premise: John has a yellow ball in his hand.
Conclusion: The yellow ball in João's hand was removed from the pot.
By abductive reasoning, the possibility that John caught the yellow ball from the pot is reasonable, but it is purely based on speculation. The yellow ball could have been, for example, bought at a store. Therefore, abducting that John took the yellow ball from the pot from the observation of the "pot full of yellow balls" may lead to a false conclusion.
Logical Reasoning Test
A logical reasoning test is a type of aptitude test widely used by employers to evaluate candidates during the recruitment process. Such tests are developed to:
- measure the ability to make logical conclusions based on information provided (typically statements or arguments)
- identify the strength of this information
These types of tests can be verbal or nonverbal, with each vendor (eg SHL, Kenexa, etc.) using their own terminology and style, making it even more confusing.
Context .vs. Logic
In logical reasoning tests examiners often ask questions where the assumptions and conclusions are obviously wrong but logically correct. Be aware that in these tests, conclusions are drawn only on the basis of logic and not on the validity of the context of the assumptions or conclusions.
Example:
Main premise: Eating too much makes you lose weight.
Minor premise: Carlos is obese.Question: What can Carlos do to lose weight?
Conclusion: Make Carlos eat a lot.
Just by context, you would think that this conclusion is incorrect, since in practice it is known that eating too much does not make you lose weight. On the contrary, you gain weight. However, based on logical reasoning, this is a valid conclusion if the assumptions are true.
In logical reasoning tests, usually the important thing is the relationship between assumptions and conclusions, not whether the content of assumptions and conclusions is in line with reality.
Formal and Informal Logical Reasoning
In logical reasoning tests, especially at higher level, additional formalism in the subject is also usually required. That includes:
- nomenclature: proposition, logical value, connectives, truth table, tautology, etc.
- symbolism: p ~ (~ p), (p Λ q) → (p → q), etc.
- theorems: non-contradiction, excluded third, etc.
- propositional and categorical logic

Comments