Como encontrar o denominador comum de duas frações?

Created on 05 Sep, 2018
Last Update on 05 Sep, 2023
1.8K views
Maintainer
Matematica

O problema de encontrar o denominador comum entre duas frações normalmente surge quando se precisa somar, subtrair ou comparar frações.
Podemos encontrar tal denominador comum calculando o MMC (“Mínimo Múltiplo Comum”) dos denominadores.

Para isso, use a calculadora online abaixo ou calcule na mão pelo dispositivo prático a seguir:


Calculadora Online: Denominador Comum
/

/

Frações Equivalentes no Denominador Comum








Dispositivo Prático de MMC

Artigo Principal: Mínimo Múltiplo Comum

Acompanhe, no exemplo abaixo, como calcular o MMC de 12 e 45 usando o dispositivo prático:

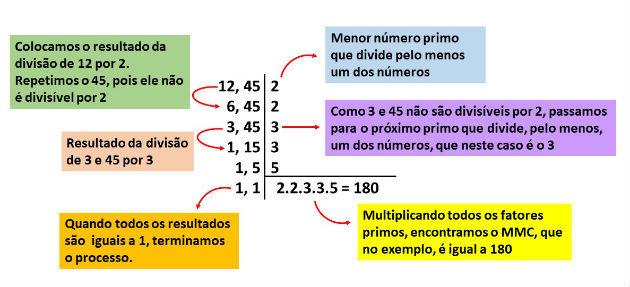
Note que:

  • Números primos são aqueles números naturais divisíveis apenas por si mesmo: 2, 3, 5, 7, 11, 17, 19 …
  • Ao final desse método, todos esses fatores primos são multiplicados entre si para obter-se que MMC(12,45) = 180.


Exemplos Aplicados

Adição

Calcule: 2/6 + 5/9 = ?

  1. Encontrar o denominador comum das frações
    Os denominadores dessas frações são 6 e 9.
    Usando a calculadora online acima obtemos que o MMC(6,9)=36.
    Portanto, o denominador comum dessas frações é 36.

  2. Encontre as frações equivalentes no denominador comum
    Divida o MMC pelo denominador e multiplique esse valor pelo numerador.

    36 ÷ 6 = 6 & 2 × 6 = 12
    => 2/6 = 12/36

    36 ÷ 9 = 4 & 5 × 4 = 20
    => 5/9 = 20/36

  3. Faça a operação normalmente com os numeradores e repita o denominador comum
    Como as frações equivalentes estão num denominador em comum, então basta somar os numeradores e repetir o denominador.

    2/6 + 5/9 = 12/36 + 20/36 = 22/36

⚠ Dica

Simplifique antes do MMC
Note que podemos simplificar a fração 2/6.
Dividindo tanto o numerador quanto denominador por 2, obtemos que 2/6 = 1/3.
Agora as contas ficam bem mais simples.


Subtração

Calcule: 8/10 - 4/12 = ?

  1. Encontrar o denominador comum das frações
    Os denominadores dessas frações são 10 e 12.
    Usando a calculadora online acima obtemos que o MMC(10,12)=60.
    Portanto, o denominador comum dessas frações é 60.

  2. Encontre as frações equivalentes no denominador comum
    Divida o MMC pelo denominador e multiplique esse valor pelo numerador.

    60 ÷ 10 = 6 & 6 × 8 = 48
    => 8/10 = 48/60

    60 ÷ 12 = 5 & 5 × 4 = 20
    => 4/12 = 20/60

  3. Faça a operação normalmente com os numeradores e repita o denominador comum
    Como as frações equivalentes estão num denominador em comum, então basta somar os numeradores e repetir o denominador.

    8/10 - 4/12 = 48/60 - 20/60 = 28/60

⚠ Dica

Simplifique antes do MMC
Note que podemos simplificar as frações 8/10 e 4/12.
Dividindo tanto o numerador quanto denominador por 2 e 4 respectivamente, obtemos que 8/10 = 4/5 e 4/12 = 1/3.
Agora as contas ficam bem mais simples.


Comparação

Compare: 2/3 é maior, menor ou equivalente a 3/5 ?

  1. Encontrar o denominador comum das frações
    Os denominadores dessas frações são 3 e 5.
    Usando a calculadora online acima obtemos que o MMC(3,5)=15.
    Portanto, o denominador comum dessas frações é 15.

  2. Encontre as frações equivalentes no denominador comum
    Divida o MMC pelo denominador e multiplique esse valor pelo numerador.

    15 ÷ 3 = 5 & 5 × 2 = 10
    => 2/3 = 10/15

    15 ÷ 5 = 3 & 3 × 3 = 9
    => 3/5 = 9/15

  3. Compare apenas os numeradores
    Como as frações equivalentes estão num denominador em comum, então basta comparar os numeradores:

    10/15 > 9/15 portanto, 2/3 > 3/5


Exercícios de Aprofundamento


Leitura Adicional
Edit
History

Replies

Comments