Prova: Exame de Matemática Enem 2019

Os movimentos ondulatórios (periódicos) são representados por equações do tipo ±Asen(ωt + θ), que apresentam parâmetros com significados físicos importantes, tais como a frequência ω = 2π/T, em que T é o período; A é a amplitude ou deslocamento máximo; θ é o ângulo de fase 0 ≤ θ < 2π/T, que mede o deslocamento no eixo horizontal em relação à origem no instante inicial do movimento.

O gráfico representa um movimento periódico, P = P(t), em centímetro, em que P é a posição da cabeça do pistão do motor de um carro em um instante t, conforme ilustra a figura.

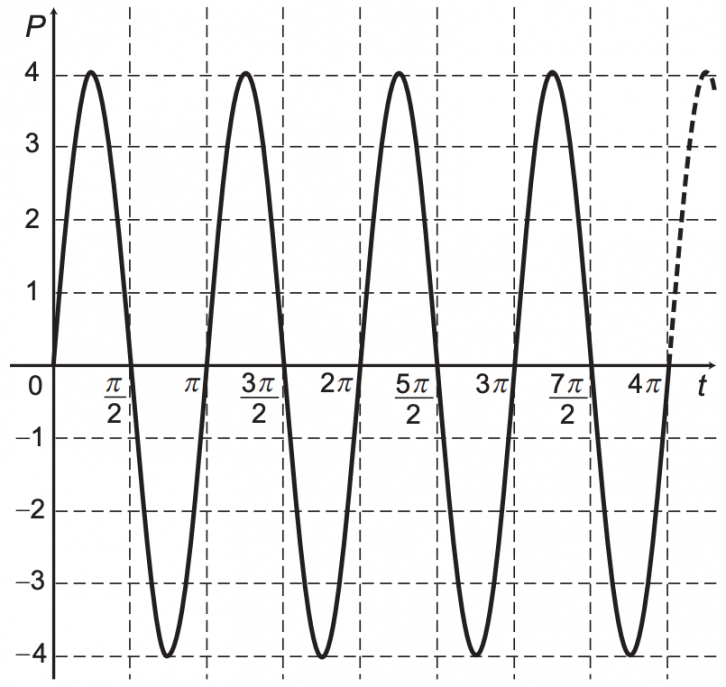
A expressão algébrica que representa a posição P(t), da cabeça do pistão, em função do tempo t é

1. P(t) = 4 sen(2t)
2. P(t) = -4 sen(2t)
3. P(t) = -4 sen(4t)
4. P(t) = 4 sen(2t + π/4)
5. P(t) = 4 sen(4t + π/4)