Enem 2022: Matemática
Prova: Exame de Matemática Enem 2022
O governo de um estado pretende realizar uma obra de infraestrutura para auxiliar na integração e no processo de escoamento da produção agrícola de duas cidades. O projeto consiste na interligação direta das cidades, A e B com a Rodovia 003, pela construção das Rodovias 001 e 002. As duas rodovias serão construídas em linha reta e deverão se conectar a Rodovia 003 em um mesmo ponto, conforme esboço apresentado na figura, na qual estão também indicadas as posições das cidades A e B, considerando o eixo x posicionado sobre a Rodovia 003, e cinco localizações sugeridas para o ponto de conexão entre as três rodovias.
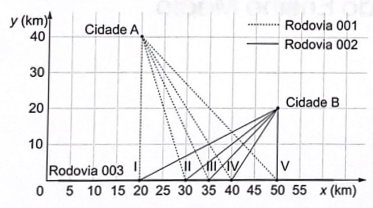
Pretende-se que a distância percorrida entre as duas cidades, pelas Rodovias 001 e 002, passando pelo ponto de conexão, seja a menor possível.
Dadas as exigências do projeto, qual das localizações sugeridas deve ser a escolhida para o ponto de conexão?
(A) I
(B) II
(C) III
(D) IV
(E) V
Resolução
Podemos calcular o comprimento das rodovias 001 e 002 usando o teorema de Pitágoras para triângulos retângulos:
c = √(a² + b²)
Daí, para cada um dos projetos teremos:
| Projeto | ΔxA | ΔyA | LA | ΔxB | ΔyB | LB | LA + LB |
|---|---|---|---|---|---|---|---|
| I | 0 | 40 | √(0² + 40²) | 30 | 20 | √(30² + 20²) | ≈76,1 |
| II | 10 | 40 | √(10² + 40²) | 20 | 20 | √(20² + 20²) | ≈69,5 |
| III | 15 | 40 | √(15² + 40²) | 15 | 20 | √(15² + 20²) | ≈67,7 |
| IV | 20 | 40 | √(20² + 40²) | 10 | 20 | √(10² + 20²) | ≈67,1 |
| V | 30 | 40 | √(30² + 40²) | 0 | 20 | √(0² + 20²) | 70 |
Ou seja, o projeto IV tem a menor distância com aproximadamente 67,1 km.
Gabarito: (D)
Enquete
O que você achou dessa questão? Fácil, Médio ou Difícil?
Deixe sua resposta nos comentários abaixo.
Comments • 0