Prova: Exame de Matemática Enem 2018
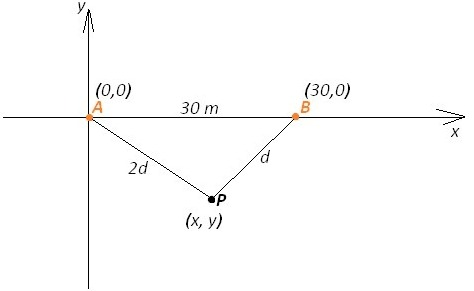
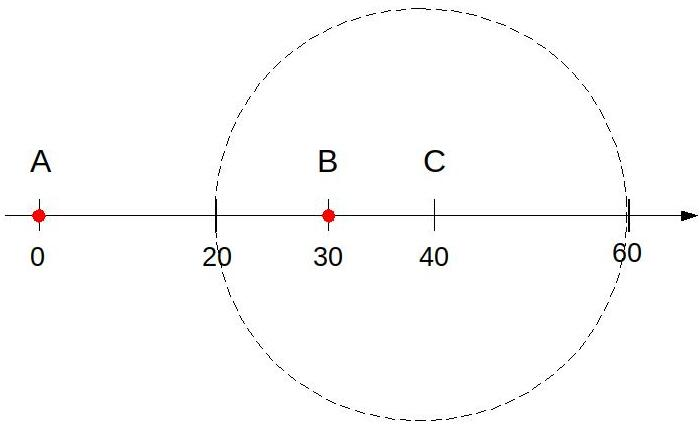
Para apagar os focos A e B de um incêndio, que estavam a uma distância de 30m um do outro, os bombeiros de um quartel decidiram se posicionar de modo que a distância de um bombeiro ao foco A, de temperatura mais elevada, fosse sempre o dobro da distância desse bombeiro ao foco B, de temperatura menos elevada.
Nestas condições, a maior distância, em metro, que dois bombeiros poderiam ter entre eles é
- 30
- 40
- 45
- 60
- 68

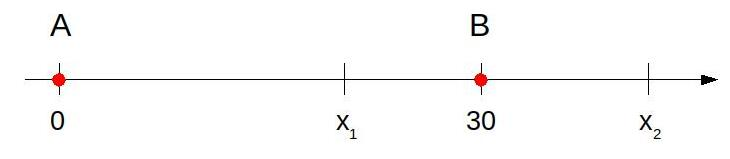

Comments