Resolução Detalhada

A ideia fundamental nesta questão é: após o desastre, e consequentemente o vazamento, como ficará o reservatório? Em outras palavras, o que ocorrerá dentro dele?

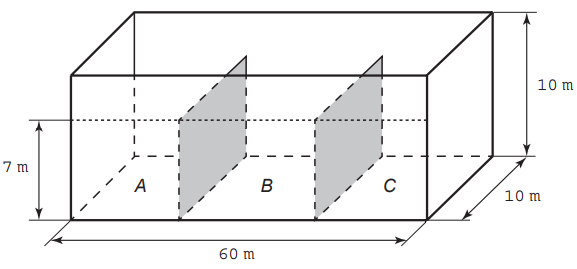
Precisamos ter claro que a estratégia adotada para minimizar o impacto ambiental em caso de derramamento é de se dividir o reservatório em 2 regiões: uma superior a 7 metros e uma inferior a 7 metros, relativos às alturas das placas de aço. Assim, em caso de rompimento, independentemente em qual compartimento seja, todo o volume da parte superior vazará. Na sequência todo o volume do compartimento que rompeu também vazará, restando apenas o volume presente nos outros dois compartimentos. Para facilitar a visualização, observe a figura abaixo que representa a vista frontal do reservatório:

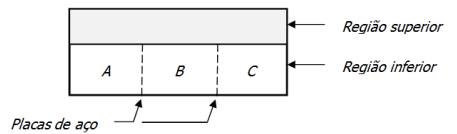
Diante desta situação podemos resolver o problema por dois métodos distintos:

• Método 1: somar o volume da região superior com o volume de um compartimento.
• Método 2: subtrair o volume de 2 compartimentos do volume total do reservatório.

Método 1

A região superior equivale a um paralelepípedo cujas dimensões são:

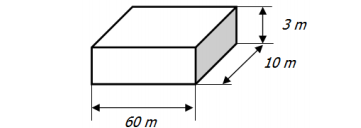
E seu volume corresponde ao produto destas dimensões:
V = 60 ∙ 10 ∙ 3 ⇒ V = 1 800 m³

Cada compartimento equivale a um paralelepípedo cujas dimensões são:

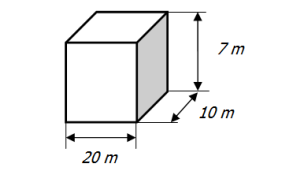
E seu volume corresponde ao produto destas dimensões:
V = 20 ∙ 10 ∙ 7 ⇒ V = 1 400 m³

Logo, após o fim do vazamento, o volume de petróleo derramado terá sido de:
1 800 + 1400 = 3,2 ∙ 10³ m³

Método 2

O reservatório equivale a um paralelepípedo cujas dimensões são:

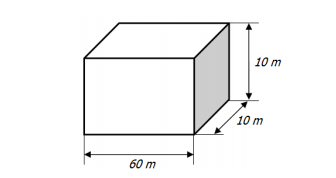
E seu volume corresponde ao produto destas dimensões:
V = 60 ∙ 10 ∙ 10 ⇒ ܸV = 6 000 m³

Como já temos o volume do compartimento calculado pelo método 1, vamos apenas multiplicá-lo por 2:
2 ∙ 1 400 = 2 800 m³

Logo, após o fim do vazamento, o volume de petróleo derramado terá sido de:
6 000 − 2 800 = 3 200 = 3,2 ∙ 10³ m³

Comentários

• Em ambos os métodos, ao final tivemos que escrever os volumes em notação científica, que é um conceito bastante importante de ser avaliado.
• A largura do compartimento, de 20 m, foi calculada pela divisão do comprimento do reservatório, que é de 60m, por 3. Afinal, são 3 compartimentos (60 ÷ 3 = 20).

Conteúdo

• Geometria Espacial (volume do paralelepípedo)
• Notação Científica

Gabarito: (D)

Gabarito: (D)

Resolução Fácil e Rápida

Volume do vazamento:

20 ⋅ 10 ⋅ 7 + 60 ⋅ 10 ⋅ 3 = 3 200 m³ = 3,2 ⋅ 10³ m³

Gabarito: (D)