Prova: Exame de Matemática Enem 2016
O tênis é um esporte em que a estratégia de jogo a ser adotada depende, entre outros fatores, de o adversário ser canhoto ou destro.
Um clube tem um grupo de 10 tenistas, sendo que 4 são canhotos e 6 são destros. O técnico do clube deseja realizar uma partida de exibição entre dois desses jogadores, porém, não poderão ser ambos canhotos.
Qual o número de possibilidades de escolha dos tenistas para a partida de exibição?
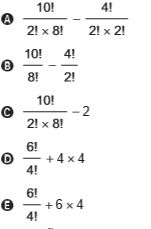


Comments